02_快速的 Redis 有哪些慢操作
Redis 的快到底是快在哪里?
一个重要的表现就是,它接收到一个键值对操作后,能以微秒级别的速度找到数据,并快速完成操作
数据库有这么多,为什么 Redis 有这么突出的表现?
- 一方面,它是内存数据库,所有操作都在内存上完成,内存的访问速度本身就很快
- 另一方面,要归功于它的数据结构
因为键值对是按一定的数据结构来组织的,操作键值对最终就是对数据结构进行增删改查操作,所以高效的数据结构是Redis快速处理数据的基础
简单来说,底层数据结构一共有 6 种,分别是简单动态字符串、双向链表、压缩列表、哈希表、调表和整数数组
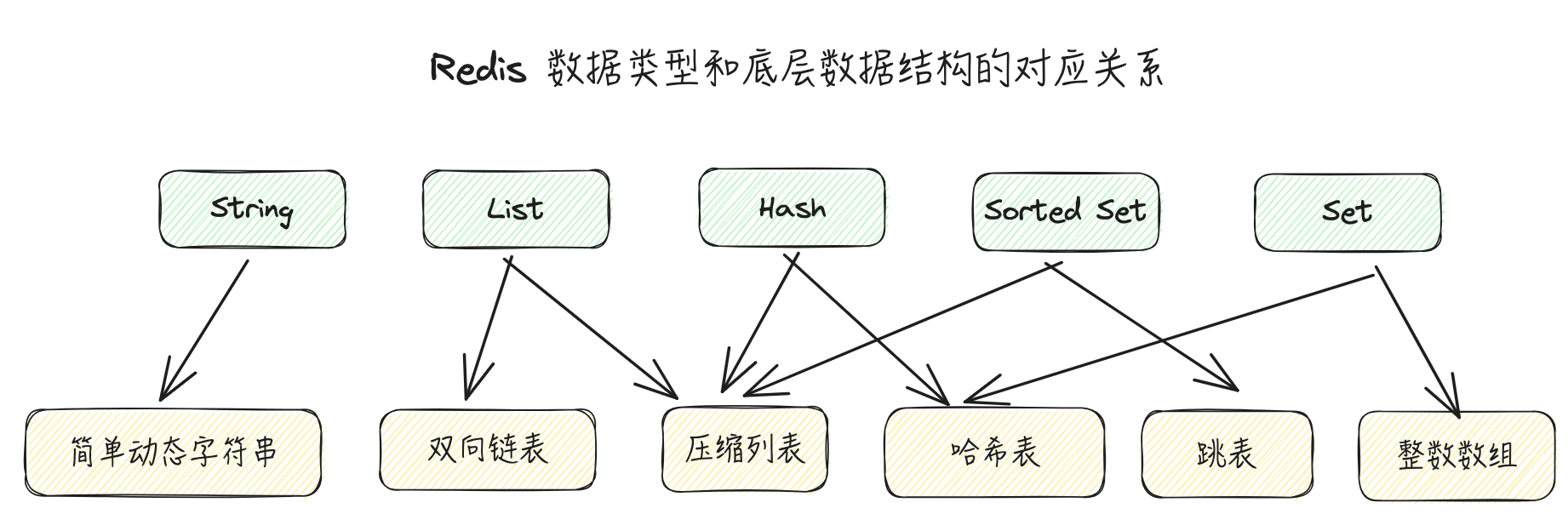
可以看到,String 类型的底层实现只有一种数据结构,也就是简单动态字符串
而 List、Hash、Set 和 Sorted Set 都有两种底层实现结构
通常情况下会把这四种类型称为集合类型,它们的特点是一个键对应了一个集合的数据
那么,问题来了
- 这些数据结构都是 Value 的底层实现,键和值本身之间用什么结构组织?
- 为什么集合类型有那么多的底层结构,它们都是怎么组织数据的,都很快吗?
- 什么是简单动态字符串,和常用的字符串是一回事吗?
键和值用什么结构组织
Redis 使用了一个哈希表来保存所有键值对
一个哈希表,其实就是一个数组,数组的每个元素称为一个哈希桶,每个哈希桶中保存了键值对数据
而且,哈希桶中的元素保存的并不是值本身,而是指向具体值的指针(不管是 String 类型还是集合类型)
查找过程主要依赖于哈希计算,和数据量的多少并没有直接关系
也就是说,不管哈希表里有 10 万个键还是 100 万个键,我们只需要一次计算就能找到相应的键
但是当你往 Redis 中写入大量数据后,就可能发现操作有时候会突然变慢了
这其实是因为我们忽略了一个潜在的风险点,那就是哈希表的冲突问题和 rehash 可能带来的操作阻塞
为什么哈希操作变慢了
当我们往哈希表中写入更多数据时,哈希冲突是不可避免的问题
也就是指,两个 Key 的哈希值和哈希桶计算对应关系时,正好落在了同一个哈希桶中
Redis 解决哈希冲突的方式,就是链式哈希
就是指同一个哈希桶中的多个元素用一个链表来保存,它们之间依次用指针连接
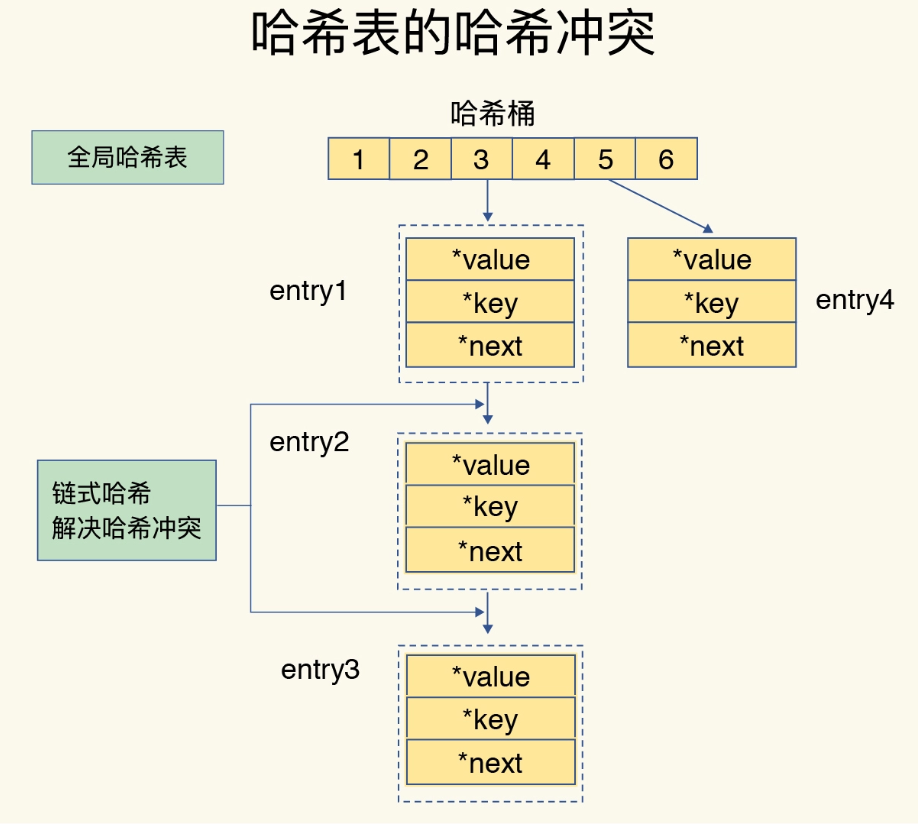
但是如果哈希表里写入的数据越来越多,哈希冲突可能也会越来越多,这就会导致某些哈希冲突链过长,进而导致这个链上的元素查找耗时长,效率降低!对于追求“快”的 Redis 来说这是不太能接受的
所以,Redis 会对哈希表做 rehash 操作
rehash 就是增加现有的哈希桶数量,让逐渐增多的 entry 元素能在更多的桶之间分散保存,减少单个桶中的元素数量,从而减少单个桶中的冲突
那么具体怎么做呢?
为了让 rehash 操作更高效,Redis 默认使用了两个全局哈希表:哈希表 1 和哈希表 2
在一开始,当我们刚插入数据时,默认使用哈希表 1,此时的哈希表 2 并没有被分配空间
随着数据逐步增多,Redis 开始执行 rehash,过程分为三步
- 给哈希表 2 分配更大的空间,例如是哈希表 1 大小的两倍
- 把哈希表 1 中的数据重新映射并拷贝到哈希表 2 中
- 释放哈希表 1 的空间
这个过程看似简单,但是第二步涉及大量的数据拷贝,如果一次性把哈希表 1 的数据都迁移完,会造成 Redis 线程阻塞,无法服务其他请求。此时,Redis 就无法快速访问数据了
为了避免这个问题,Redis 采用了渐进式 rehash
简单来说就是在第二步拷贝数据时,Redis 仍然正常处理客户端请求,每处理一个请求时,从哈希表 1 中的第一个索引位置开始,顺带着将这个索引位置上的所有 entries 拷贝到哈希表 2 中;等处理下一个请求时,再顺带拷贝哈希表 1 中的下一个索引位置的 entries
渐进式 rehash 巧妙地把一次性大量拷贝的开销,分摊到了多次处理请求的过程中,避免了耗时操作,保证了数据的快速访问
集合数据操作效率
和 String 类型不同,一个集合类型的值,第一步是通过全局哈希表找到对应的哈希桶位置,第二步是在集合中再增删改查
那么,集合的操作效率和哪些因素有关呢?
首先,与集合的底层数据结构有关。例如,使用哈希表实现的集合,要比使用链表实现的集合访问效率更高。其次,操作效率和这些操作本身的执行特点有关,比如读写一个元素的操作要比读写所有元素的效率高
有哪些底层数据结构?
集合类型的底层数据结构主要有 5 种:整数数组、双向链表、哈希表、压缩列表和跳表
哈希表的操作特点比较简单,不多做介绍;整数数组和双向链表也很常见,操作特征都是顺序读写,也就是通过数组下标或者链表的指针逐个元素访问,操作复杂度基本是 O(N),操作效率比较低
重点解释一下压缩列表和跳表
压缩列表
压缩列表类似于一个数组,数组中的每一个元素都对应保存一个数据。和数组不同的是,压缩列表在表头有三个字段 zlbytes、zltail、zllen,分别表示列表长度、列表尾的偏移量和列表中的 entry 个数;压缩列表在表尾还有一个 zlend,表示列表结束
在压缩列表中,如果我们要查找定位第一个元素和最后一个元素,可以通过表头三个字段的长度直接定位,复杂度是 O(1);而查找其他元素时,就没有这么高效了,只能逐个查找,此时的复杂度就是 O(N)

跳表
有序链表只能逐一查找元素,导致操作起来非常缓慢,于是出现了跳表
具体来说,跳表在链表的基础上,增加了多级索引,通过索引位置的几个跳转,实现数据的快速定位
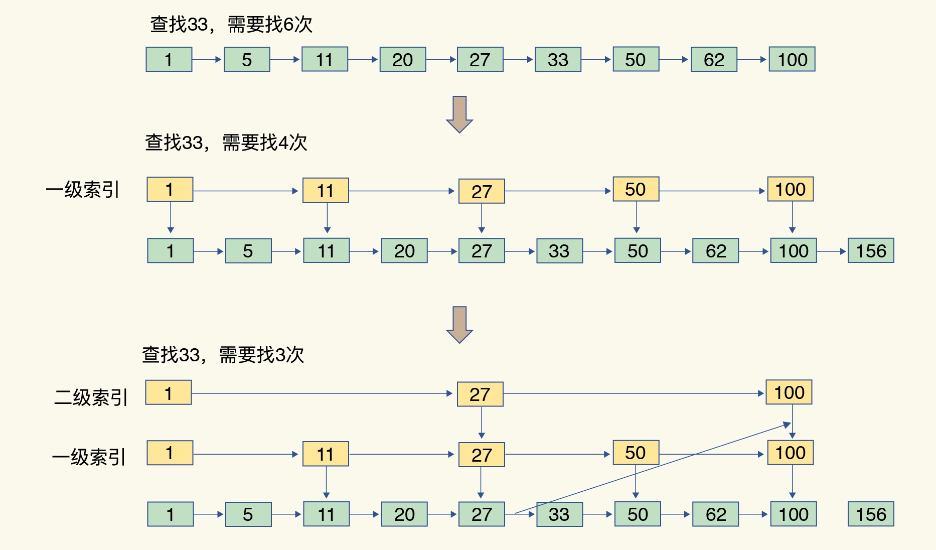
可以看出,查找数据的过程在多级索引上跳来跳去,最后定位到元素,这也符合跳表的叫法,当数据量很大时,跳表的查找复杂度就是 O(logN)
按照查找的时间复杂度给这些数据结构分下类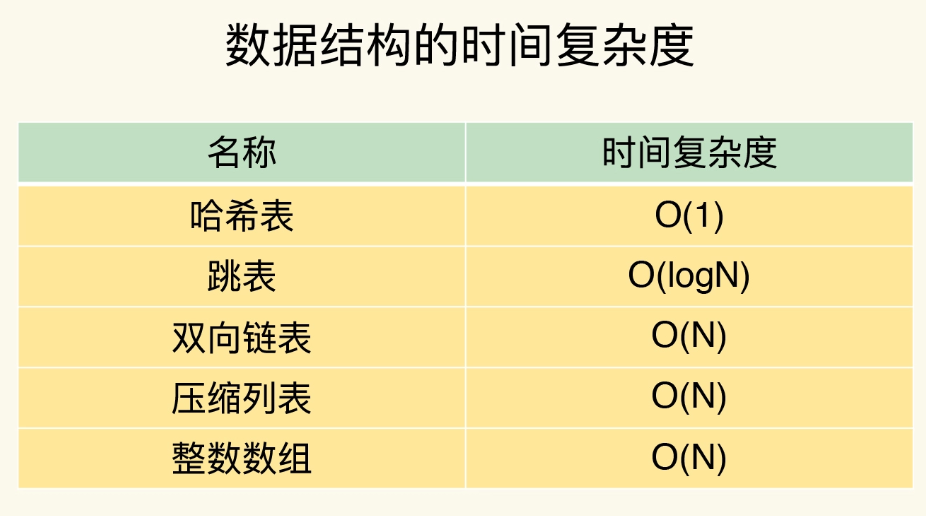
不同操作的复杂度
集合类型的操作类型有很多
- 有读写单个集合元素,例如 HGET、HSET
- 有操作多个元素的,例如 SADD
- 有对整个集合进行遍历操作的,例如 SMEMBERS
它们的复杂度各不相同,而复杂度的高低又是我们选择集合类型的重要依据
极客老师总结了四句口诀
- 单元素操作是基础
- 范围操作非常耗时
- 统计操作通常高效
- 例外情况只有几个
# 单元素操作
指每一种集合类型对单个数据实现的增删改查操作
例如,Hash 类型的 HGET、HSET 和 HDEL
# 范围操作
指集合的遍历操作,可以返回集合中的所有数据
例如,Hash 类型的 HGETALL,SET 类型的 SMEMBERS
这类操作的复杂度一般是 O(N),比较耗时,尽量避免
# 统计操作
指集合类型对集合中所有元素个数的记录
例如 LLEN、SCARD,这类操作复杂度只有 O(1),因为当集合类型采用压缩列表、双向链表、整数数组这些数据结构时,这些结构中专门记录了元素的个数统计,因此可以高效地完成相关操作
# 例外情况
指某些数据结构的特殊记录,例如压缩列表和双向链表都会记录表头和表尾的偏移量
对于 List 类型的 LPOP、RPOP、LPUSH、RPUSH 这四个操作来说,它们是在列表的头尾增删元素,这就可以通过偏移量直接定位,所以复杂度也是 O(1)